Generalizing a Tree Canopy Drawing

• Original Paper
• Open Access
• Published: 06 February 2017

Reconstructing forest canopy from the 3D triangulations of airborne laser scanning point data for the visualization and planning of forested landscapes

Annals of Forest Science volume 74, Article number:9 (2017) Cite this article

• 2520 Accesses

• 4 Citations

• 11 Altmetric

• Metrics details

Abstract

Key message

We present a data-driven technique to visualize forest landscapes and simulate their future development according to alternative management scenarios. Gentle harvesting intensities were preferred for maintaining scenic values in a test of eliciting public's preferences based on the simulated landscapes.

Context

Visualizations of future forest landscapes according to alternative management scenarios are useful for eliciting stakeholders' preferences on the alternatives. However, conventional computer visualizations require laborious tree-wise measurements or simulators to generate these observations.

Aims

We describe and evaluate an alternative approach, in which the visualization is based on reconstructing forest canopy from sparse density, leaf-off airborne laser scanning data.

Methods

Computational geometry was employed to generate filtrations, i.e., ordered sets of simplices belonging to the three-dimensional triangulations of the point data. An appropriate degree of filtering was determined by analyzing the topological persistence of the filtrations. The topology was further utilized to simulate changes to canopy biomass, resembling harvests with varying retention levels. Relative priorities of recreational and scenic values of the harvests were estimated based on pairwise comparisons and analytic hierarchy process (AHP).

Results

The canopy elements were co-located with the tree stems measured in the field, and the visualizations derived from the entire landscape showed reasonably realistic, despite a low numerical correspondence with plot-level forest attributes. The potential and limitations to improve the proposed parameterization are discussed.

Conclusion

Although the criteria to evaluate the landscape visualization and simulation models were not conclusive, the results suggest that forest scenes may be feasibly reconstructed based on data already covering broad areas and readily available for practical applications.

Introduction

Environmental and forestry decision making requires the identification and comparisons of different management alternatives based on multiple objectives and stakeholders (Kangas et al. 2008). Integrating information on the impacts of management decisions with preferences of the stakeholders results in a framework called multiple criteria decision analysis (MCDA). When incorporated with a geographic information system (GIS), the resulting applications are nowadays called "spatial MCDA" or "public participation geographic information system" (PPGIS; Sieber 2006), depending on the involvement of the stakeholder. Early forestry applications of spatial MCDA and PPGIS are provided by Store and Kangas (2001) and Kangas and Store (2003), respectively.

Projecting future forest landscapes according to alternative management scenarios is a particularly useful MCDA component for participatory forest planning. For example, impacts of growth, management practices, forest (logging) operations, and locations of logging areas may affect the stakeholders' preferences on the management alternatives. It has long been recognized that even technically simple computer visualizations improve understanding of forest stand dynamics and effects of management decisions (Pukkala and Kellomäki 1988; Burkhart 1992) and facilitate eliciting the related preferences (Tahvanainen et al. 2001; Karjalainen and Tyrväinen 2002). Visualization techniques and applications are reviewed in the forestry context by Mendoza et al. (2006) and Falcão (2008) and techniques for extracting the decision makers' preferences from the visualizations by Kangas et al. (2008). Recent practical examples of incorporating the information obtained in decision support and GIS frameworks are presented by Warren-Kretzschmar and von Haaren (2014) and Lämås et al. (2015).

The visualizations of forested landscapes require balancing between the image realism, the desired resolution, and the measurements available (cf. Bergen et al. 1998; Uusitalo and Orland 2001). Even if extremely photorealistic forest scenes may be obtained by combining botanical models of tree architecture with line graphics or real tree textures presented in virtual reality environments (e.g., Aono and Kunii 1984; Honjo and Lim 2001; Fujisaki et al. 2008), the tree and branch-level measurements required by these techniques are time-consuming and expensive. Unless tree-wise inventory data are available, the landscapes need to be populated with trees based on less detailed inventory data. A typical approach is to simulate the locations and appearances of the individual trees based on mean diameter, height, and structure information (e.g., Karjalainen and Tyrväinen 2002). Particularly, the use of mean-based attributes and thus the requirement to simulate the trees will result in generalizations and restrictions of reality (Uusitalo and Orland 2001; Wang et al. 2006).

Techniques based on remote sensing provide significant advances over conventional forest measurements. Particularly due to its capability to present forest structure as a point cloud mapped in 3D, airborne laser scanning (ALS; also referred to in some instances as "airborne scanning LiDAR") has become an increasingly popular technique for various forestry applications (Maltamo et al. 2014). However, the use of ALS for visualizing forestry decision making has been rare, to date, even though proposed already by Hill and Veitch (2002), McGaughey and Carson (2003), and Ahlberg et al. (2004). Despite the availability of feature-rich software packages for visualizing ALS point clouds, rendering realistic tree geometry from the point data poses a problem (Simons et al. 2014). Typical approaches to parameterize a forest scene in ALS-based analyses include populating a list of tree locations and dimensions using simple artificial turbid media such as cones, ellipses, voxels (Schneider et al. 2014), or other types of 3D primitives (Koch et al. 2014). A common problem of these approaches is, however, the requirement for a very high data density (e.g., tens of pulses per m²), whereas practically available data sets are typically collected for other purposes such as ground elevation modeling with densities as low as <1 pulses per m² (e.g., Nord-Larsen and Schumacher 2012; Villikka et al. 2012).

Triangulating point data and subsequent filtering of the triangulations (e.g., Delfinado and Edelsbrunner 1995) has been proposed as an alternative means to represent the 3D canopy surface (Vauhkonen et al. 2014). As opposed to approaches that use fixed image elements and therefore require specifying an artificial pixel or voxel resolution, the triangulations are entirely based on the properties of the point data. Applying filtrations, one can adjust the level of detail in the triangulated point cloud and thus account for canopy gaps and detailed properties existing in the data (see Sect. 2.2. for details). The optimal degree of filtering is found to be forest structure specific (Vauhkonen et al. 2016), whereas less detailed information could suffice for generating realistic visualizations of tessellated landscapes (Vauhkonen 2015). We additionally propose that the topology based on the filtrations could be utilized as a mechanism to simulate changes in the forested landscapes visualized (Sect. 2.3.), which is complicated based on simulated forest stand dynamics (cf. Dreyfus 2012).

Even though the low resolution obtainable by the practically available sparse data most likely restricts the detail of the visualizations, the decision maker may be expected to benefit from representing real tree geometry (cf. Uusitalo and Orland 2001) and visual descriptions (cf. Tahvanainen et al. 2001) instead of simulated and verbally or numerically described forest scenes. Another practical benefit of our approach is that required data can be feasibly extracted from any location covered by an ALS campaign such as those designed for collecting sparse density data for ground elevation modeling. Although the suitability of such data for forest inventories was verified (Nord-Larsen and Schumacher 2012; Villikka et al. 2012), the benefits of using the spatially explicit 3D scenes obtainable have not been fully employed despite the potential identified earlier (Hill and Veitch 2002; McGaughey and Carson 2003; Ahlberg et al. 2004). Therefore, rather than developing another virtual reality platform aiming at improved photorealism with high costs of collecting the required data, we present a wireframe model on how to extract information from the visualized forest scenes for a spatial MCDA to open up discussion on the potential and limitations of the broadly available sparse ALS point data to support forestry decision making.

The purpose of this study is to describe a technique for visualizing forest scenes from sparse density ALS data and evaluate their potential for forestry decision support, making a difference between (i) close-range and (ii) landscape levels. The close-range visualizations correspond to a within-forest view and up to a plot scale, whereas the landscape level shows forest areas in scales of tens to hundreds of hectares corresponding to typical properties managed by a single forest owner. The forest scenes were obtained applying a triangulating and filtering technique to ALS data acquired originally for ground elevation modeling. Regarding (i), we assessed the correspondence of the forest canopy elements modeled as tetrahedra and obtained by filtering the triangulations with forest attributes observed in the field. Regarding (ii), we introduce an intuitive concept based on using the filtrations to simulate changes to canopy biomass. The initial and simulated landscapes are visualized and demonstrated in eliciting public's preferences on scenic values resulting from biomass harvests applied with varying intensities.

Material and methods

Study area and data

The study area is a typical, managed boreal forest in eastern Finland. An area of 1000 × 1200 m located approximately on 62° 31.5′ N, 30° 11′ E was selected for the visualizations due to the presence of a forest and lake mosaic, which likely produced high recreational and scenic values over the area. The data for the visualizations included the locations of the lakes and ALS data extracted from a topographic database. In addition, the ALS data were extracted for a number of field sample plots existing in the area, and the field measurements co-located with the ALS data were used to assess the correspondence of the modeled canopy with respect to the field data. The plots were located up to 2.5 km apart the visualized area and were earlier used to study the spatial pattern and diameter distribution of the trees from both the ecological and economic perspectives. Scots pine (Pinus sylvestris L.) and Norway spruce (Picea abies [L.] Karst.), with a minor proportion of deciduous species, were present in the plots, whereas the area used for the visualizations was assumed to be nearly purely pine-dominated.

The ALS data used in the study were acquired by the National Land Survey of Finland as a part of their data acquisition campaign for creating a nationwide ground elevation model for Finland. The data were downloaded from a file service (https://tiedostopalvelu.maanmittauslaitos.fi/tp/kartta?lang=en), from which they are available for free and with extensive permissions of use. The data were acquired on April 30, 2012, with Leica ALS60 scanner operated in a multipulse mode. The flying altitude was 2350 m, yielding a nominal pulse density of 0.8 m⁻². The data provider had detected and classified the ground level, on which the normalization of the vegetation height values was based. As the data are meant specifically for ground elevation modeling, we assumed the accuracy of this classification to be appropriate for our purposes. The analyses were focused only on the first echoes (i.e., "only" and "first of many" of up to four echoes recorded per pulse), aiming to obtain the main information from the data (Vauhkonen et al. 2014), while retaining most generalization abilities over sensors that record a different number of echo categories (e.g., Næsset 2014).

The field plots were measured in May–June, 2010. All trees with either diameter at breast height (DBH) ≥ 4 cm or height ≥ 4 m were mapped for locations and measured for species, DBH, and height. The measurements are described in more detail by Packalén et al. (2013). For simplicity, the plot size used in this study was standardized to 400 m², rather than varying from 400 to 900 m² as in the earlier publications. The standardization was achieved by creating rectangular windows of 20 × 20 m with the center and orientation corresponding to the original plot. The trees located within this window based on the measured tree coordinates were extracted for the analyses.

Plot-level basal area was computed based on summing from the diameter measurements. Dominant height was determined as the mean height of 100 thickest trees per hectare (four trees per plot). Individual stem volumes were estimated by models of Laasasenaho (1982), employing the DBH, height, and tree species as predictors. The models for birch were used for all deciduous trees. The spatial pattern of the trees was assessed by means of the Clark-Evans index (CEI; Clark and Evans 1954) of the aggregation of a point pattern. The CEI values were computed based on the tree coordinates using the spatstat package of the R statistical computing environment (Baddeley and Turner 2005), applying an edge correction proposed by Donnelly (1978). General descriptive statistics of the field data are shown in Table 1.

Table 1 Central characteristics of the 71 field plots

Full size table

Modeling the initial forest canopy using triangulations

In our approach, "visualization" essentially refers to visualizing forest canopy geometry based on the 3D measurements collected by an ALS sensor (e.g., Sun and Ranson 2000). The geometry is composed of n-dimensional basic elements (points, edges, facets, tetrahedra), which are referred to using generic term "simplex" unless an element of a specific dimension is particularly denoted. The main canopy elements are tetrahedra obtained by subdividing the underlying space of the 3D measurements, which is called triangulating. The entire triangulation, referred to below also as "complex," thus represents both the canopy and empty space, which need to be divided to separate subcomplexes constructing a filter. The triangulations were filtered using a well-known computational geometric or topological concept called 3D alpha shapes (Edelsbrunner and Mücke 1994), while an appropriate degree of filtering was determined by analyzing persistence of the observed topology, i.e., topological persistence or persistent homology (Edelsbrunner et al. 2002). All computations were based on Delaunay triangulations and implemented with C++ and open-source libraries (Morozov 2012; Da et al. 2013; Pion and Teillaud 2013). The applied workflow is described below, but the mathematical formalism is intentionally left to the original publications. Illustrations of all the concepts applied to ALS data are presented by Vauhkonen (2015), for example.

Following earlier analyses with ALS point data (Vauhkonen et al. 2014, 2016), the landscape was tessellated to a regular grid with a cell size corresponding to the plot size (20 × 20 m). The ALS data of each cell or plot was triangulated and filtered separately. The problem related to using the alpha shapes is the determination of a proper value for alpha (α), which is a threshold for the squared radius of the circumscribing sphere of each simplex and therefore a criterion determining which simplices of the full triangulation belong to its current subcomplex, i.e., α-complex or α-shape. Here, the value of α was selected based on filtration obtained by ordering the α-complexes according to the values of α (see also Delfinado and Edelsbrunner 1995).

During the filtration, i.e., by increasing the value of α, simplices of a dimension d join together with other d-dimensional simplices to form structures with a higher dimensionality. Particularly, when the value of α allows two points (d = 0) to connect, an edge of d = 1 between these two points is formed. The edges further join to form facets (d = 2) and tetrahedra (d = 3), the latter being the highest dimension considered here. Each simplex can thus be described by its persistence in the structure formed. This index of persistence was obtained as the absolute difference between the index values of α causing the birth and death of simplices of the given dimension.

Following the logic of the previous paragraph, a birth and death diagram was computed for indices with d = 1 and d = 2. Only these dimensions need to be considered, since those with d = 0 or d = 3 do not born or die, respectively, in this process. In the diagram, the most interesting observations are those off-diagonal: These simplices are interpret to cause the most fundamental changes to the triangulated structure, typically at the lowest values of α, while the diagonality of the observations indicates stability (persistence) of those features. The maximum off-diagonal α at the death of both d = 1 and d = 2 was hypothesized to reflect the primary persisting structures of the obtained triangulation and was thus used as the α value determining the degree of filtering and thus the initial state of the forest canopy.

The rationality of the obtained canopy was evaluated using the field data. The observed tree (stem) positions and dimensions were visualized with the canopy to assess the co-location of these elements. Descriptive characteristics were extracted from the triangulation-based canopy models and related with the forest attributes measured in the field (Table 1). The value of the parameter α resulting from the persistent homology analysis and the total tetrahedral volume, percent of the plot area covered by the tetrahedral, and top height of the underlying space of the specified α-complex were extracted, assuming these to be related to the total tree attributes of a field plot. Additionally, the number of connected tetrahedra with at least one joint edge was computed, assuming this to be related to the number of tree patches within the plot. The correspondence was assessed by means of the coefficient of determination (R ²).

Simulating changes to the canopy and assessing their impacts to the scenery

Visualizing the landscape and harvests of canopy biomass

The full landscapes were visualized using triangulation representation (TriRep) and triangular surface plot (trisurf) functions implemented in Matlab, version R2012a (MathWorks, Inc., Natick, MA, USA). The landscapes were composed of the adjacent 20 × 20 m cells processed according to Sect. 2.2. Due to depicting solely canopy geometry, certain simplifications to the visualizing other elements were adopted. The number or the spatial pattern of the tree stems could not be precisely modeled, which is a typical result of ALS-based analyses (e.g., Packalén et al. 2013). However, the landscape-level visualizations were found to be more realistic with at least some shadowing caused by the stems. A number of the highest tetrahedra per cell were thus accompanied with simulated tree stems. The number of stems was determined as ceil(n _p × f × V _p /H _p ), where n _p was the number of tetrahedra, V _p was the total volume of these tetrahedra, H _p was the maximum ALS height value of the cell p, and f was a unit area factor, in this case 1/400. The diameters of the stems (in meters) were simulated as H _t /50, where H _t is the maximum height of the considered stem t in meters. The applied rules resulted in too few and too large trees, in general, but provided the landscapes with such a realism that only the largest tree stems were visible when looking from a distance. The produced landscapes were colored as pure pine forests, i.e., species recognition was not attempted due to the low proportion of other species. The ground level was depicted as perfectly flat, since the fluctuations in the terrain elevation were known to be minor in this area.

In addition to visualizing the initial canopy, reductions to the canopy volume were simulated to portray harvests with varying intensities. In the approach, simplices belonging to the canopy were re-assigned as empty space by adjusting the value of α parameter (see Sect. 2.2.) downwards. As a result, the initial α-complexes were subtracted starting from the largest tetrahedra, assuming this to correspond with harvests with varying retention levels based on removing the largest trees from the forest. The harvests were focused on one compartment with a dense initial canopy. Altogether, five harvesting intensities were defined by multiplying the initial α by a factor of 0.95, 0.75, 0.68, 0.6, and 0.5, which corresponded to an average reduction of 17, 71, 83, 93, and 99%, respectively, of the initial canopy volume (11,673 m³/ha on the area of the full compartment, on average). The visualizations of the full landscape obtained as a result of the harvesting were labeled as images A–E according to the increasing harvesting intensity and are presented as Electronic Supplementary Material (Online Resource 1).

Pairwise comparisons of the simulated landscapes

To obtain preference information on how the harvesting affected the landscape, a pairwise comparison of the visualized landscapes was implemented using the SurveyMonkey® online platform (http://www.surveymonkey.com/). In the survey, two simulated landscapes were shown at the time, asking a question of which of the two images was better with respect to the recreational use and the scenic values of the landscape and how much better it was. The respondent was asked to express his/her opinion on whether either image was (i) equally good, (ii) slightly better, (iii) clearly better, (iv) considerably/strongly better, or (v) absolutely better compared to the other. In the following text, this decision is called the priority ratio of the respondent between the two landscapes.

A link to the survey was submitted to the mailing list of the forestry students of the University of Eastern Finland and accompanied with brief instructions (translated from Finnish):

"The central compartment of [this] landscape is marked to be harvested. A walking trail and a 'laavu' (a temporary shelter for field lunch or camping) are situated in the area of the compartment. The harvesting intensity is not yet determined, but the aim is to maintain the recreational value of the forest as high as possible.

In the survey, you are asked to compare two alternative landscapes and select which harvesting intensity is better suited with respect to the recreational use and scenic values. The compartment to be harvested is delineated with a red boundary in the image below. The other parts of the landscape will not be affected. Start the survey by clicking 'Next image pair' button."

The survey was held open between 21 January and 12 February, 2015. The survey yielded altogether 57 responses, of which 7 were incomplete (no response to one or more comparisons). Altogether, 50 responses were thus analyzed in the further study.

Preference elicitation

On the basis of the pairwise comparisons (Sect. 2.3.2.), relative priorities of the scenic values with respect to the harvest intensities were estimated using the eigenvalue technique of analytic hierarchy process (AHP; Saaty 1977, 1980). This technique was used to convert verbal evaluations to ratio-scale numerical values in a forestry decision support application bearing a close resemblance to our study (Kangas et al. 1993).

In the approach, the priority ratios i–v (Sect. 2.3.2.) are translated into numerical values of 1:1, 3:1, 5:1, 7:1, and 9:1, respectively. The values are arranged into a reciprocal matrix A , and using the matrix as input, the numeric weights or priorities of the pairwise comparisons are computed as the right eigenvector of the largest eigenvalue (λ _max) of A (Saaty 1977).

To assess the coherence of the pairwise comparisons, a consistency index (CI; Saaty 1980), which estimates the level of consistency with respect to the entire comparison process, is derived by relating the value of λ _max with the number of comparisons made. The observed CI is further compared with an average CI obtained by randomly generated comparisons in a matrix with a size corresponding to A (Saaty 1980). The result is a consistency ratio (CR), which measures the coherence on a scale of 0.1. According to a general rule of thumb, comparisons with CR > 0.1 are deemed inconsistent.

Results

Except for top height, the triangulated and filtered canopy models were in low correspondence with any forest attribute when evaluated with respect to the field measurements. Nevertheless, the R ² values for the total volume and top height of the canopy model in particular were statistically significant (Table 2), and the forest structure affected the models obtained in the way it was expected. The spatial pattern of the trees, quantified in terms of CEI, significantly affected the values of the α parameter (Table 2), indicating that a different α value was required for different spatial patterns. The total tetrahedral volume of the reconstructed canopy was significantly related to all other size and structure attributes expect for the stem number (Table 2), and the volume increased according to increasing values of these attributes. The number of connected tetrahedra and the coverage of the tetrahedra relative to the plot area however had a low degree of determination with any of the field attributes. The top height of the canopy model had the best overall correspondence with the field attributes and a strong linear relationship especially with the dominant tree height. Noting that no allometric knowledge was used in the construction of the canopy, the models based on the geometry and topology of the point data still reflect the variation in the forest properties and aggregated stem attributes.

Table 2 The degree of determination (R ²) between selected field attributes and alpha value (α), total volume (V), number of connected tetrahedra (N), coverage (C), and top height (H) of the canopy models

Full size table

Based on a visual assessment, the canopy elements of the coniferous dominant canopy in particular were fairly accurately co-located with the tree stems measured in the field (Fig. 1). The positions of the canopy elements were also somewhat in line with the spatial patterns of the field measured trees, particularly those showing clustered patterns. Nevertheless, Fig. 1 also shows the limitations of the proposed technique toward close-range visualizations. The level of detail and the representation of the deciduous and understorey trees are in particular limited, the reasons of which are further discussed in Sect. 4.

Fig. 1

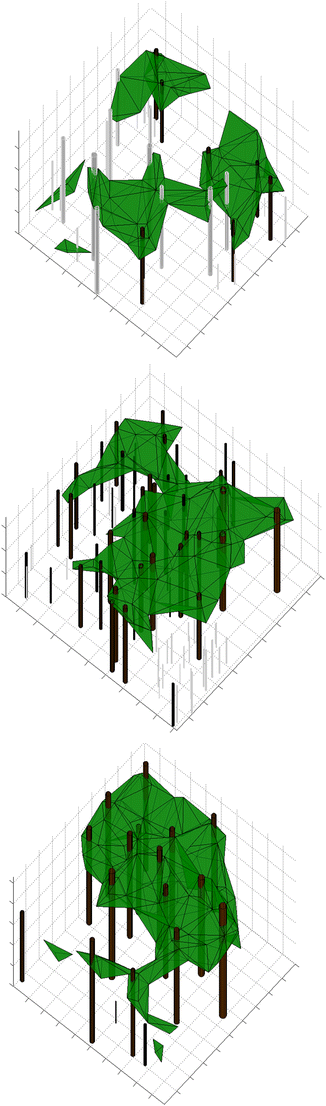
Examples of visualized plots with clustered (CEI = 0.7, above), random (CEI = 1.0, middle), and regular (CEI = 1.4, below) patterns of tree stems. The locations and dimensions of the cylinders correspond with the tree stems measured in the field. The brown and gray cylinders represent scots pine and deciduous trees, respectively. The interval between tick marks corresponds to 5 m in the vertical axis and 2 m in the plane

Full size image

Despite the low detail in close-range visualizations (Fig. 1), the visualizations derived for the entire landscape showed a reasonable level of detail and realism (Fig. 2). For instance, roads, electric lines, or otherwise open areas could be pointed out from the image. Further, despite the potential to edge effects, i.e., incorrectly cutting the ALS data due to an edge of a cell (Fig. 1), the borders of the 20 × 20 m cells did not show in the visualization of the full landscape (Fig. 2).

Fig. 2

The full landscape visualized with the approach proposed. The sub-figures on the right give examples on harvests simulated to the compartment in the center of the landscape. All five simulated landscapes are presented as Electronic Supplementary Material (Online Resource 1)

Full size image

The canopy biomass reductions simulated to the landscape were found to reasonably resemble effects of real-world harvesting operations (Fig. 2). However, the simulated harvests clearly had a more considerable effect on the horizontal coverage than on the height of the modeled canopy (Fig. 3). Especially, the top height changed very moderately based on harvesting intensities A, B, and C according to Fig. 3, which shows the effects of the simulated reduction of parameter α to the vertical and horizontal structure of the landscape.

Fig. 3

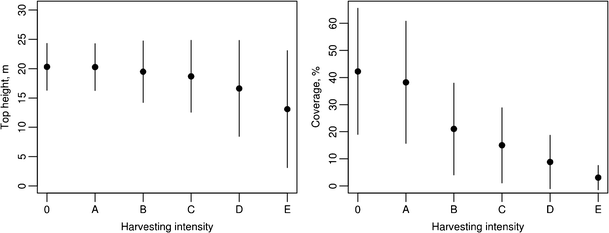
The effects of the simulated reduction of parameter α to the top height and proportion of the plot area covered by the tetrahedra of the modeled canopy. The dots and lines indicate the mean and standard deviation, respectively, within the area. Harvesting intensity 0 corresponds to the initial canopy

Full size image

According to the survey, the landscape treated with heavy harvesting intensities (images E and D) was preferred by none of the responders, while lower intensities (images C, B, and A) were selected as most preferable by 10 (20%), 16 (32%), and 24 (48%) responders, respectively. Due to these preferences, the (accumulation of) relative priority between the landscapes was significantly indifferent for different types of responders (Fig. 4) and the general trend was difficult to model without additional information.

Fig. 4

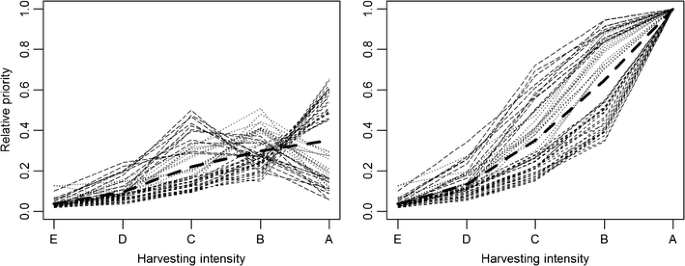
The distribution (left) and accumulation of the relative preferences between harvesting intensities. The thick line depicts the mean of all preferences. The dashing of the individual preferences varies according to which harvesting intensity was preferred most

Full size image

According to the AHP, the consistencies of the responses varied considerably. Only 10 (20%) of the pairwise comparisons had a CR < 0.1, while 30 (60%) and 10 (20%) resulted in CRs between 0.1–0.3 and >0.3, respectively. The maximum and mean CR values were 0.99 and 0.22. When examined against the relative priorities (Fig. 4), the inconsistencies were neither clustered in any preference group nor reflected in any other particular way, however.

Discussion

According to the results presented above, the canopy models and visualizations based on the sparse density ALS data are mainly suited for landscape-level analyses. The low degree of determination between the close-range models and forest attributes indicates that either a field sample to optimize the canopy model (Vauhkonen et al. 2014, 2016) or a completely different approach based on higher density data obtained by ALS or terrestrial laser scanning is required for detailed modeling. On the other hand, the proposed approach appears interesting due to the possibility to generate the visualizations from very sparse ALS data that often readily exist and the inherent property of the modeling technique to simulate changes to the landscape by adjusting the filtration parameter α. The obtained visualizations are affected by both input data and proper selection of the value for α, as discussed below.

As opposed to conventional forest visualization techniques that require laborious tree-by-tree measurements or the use of simulators to generate these observations, the present study requires a wall-to-wall coverage of ALS data over the landscape to be visualized. While the acquisitions of ALS data for ground elevation modeling nowadays allow applications of these data for vast areas, properties such as the scarcity of the input point data may restrict some forestry analyses (e.g., Vauhkonen et al. 2016). As seen from Fig. 1 of this study, for instance, the true canopy height was underestimated due to the penetration of the pulses through the top canopy (Gaveau and Hill 2003). Nevertheless, the top height extracted from the triangulation-based canopy models had a strong relationship with the dominant height (Table 2), which was comparable to the height metrics extracted from the initial point data (detailed results not shown). No information related to the spatial pattern of the trees or tree number could be derived, which is in line with earlier studies based on ALS data (e.g., Packalén et al. 2013). The percent coverage of the tetrahedra could be compared to the canopy cover metric computed from the point data as the proportion of the echoes above a certain height threshold to all echoes (Korhonen et al. 2011). This metric had a correlation of 0.8 with the tetrahedral coverage, but similarly low degrees of determination with the field-measured forest attributes.

Since the data were captured under a leaf-off period of the vegetation phenology, less first-return data were obtained from the deciduous than coniferous trees, even if those were located in the dominant canopy (Fig. 1; see also Villikka et al. 2012). Also, only limited information was obtained from the understorey. Although some researchers have detected more trees under leaf-off than leaf-on conditions, when focusing on individual tree detection in dense ALS data (Duncanson et al. 2014), also the results of Korpela et al. (2012) indicate that direct measures of the understorey are difficult to obtain due to transmission losses occurring in the upper canopy (see also Maltamo et al. 2005). For the reasons stated above, the spatial patterns of the deciduous and understorey trees may be incorrect in some parts of the landscape, but this was not assumed to be a major problem in the pine-dominated test area considered in our study. Whether attempted in more complex canopies in further studies, however, considerations on, e.g., the species and pulse penetration properties are required.

Whether the limitations described in the previous paragraph are accepted, the presented approach is proposed feasible for visualizing landscapes such as that presented in Fig. 2. The methodology presented here allows a description that is based on real canopy elements, as extracted from the triangulations based on ALS data, but not explicit prescription of leaf or shoot locations and orientations, for example. Therefore, regarding the degree of detail in describing the distribution of canopy elements, the proposed approach is a compromise between artificial tree/crown-level turbid media parameterized by a list of tree locations and dimensions (e.g., Schneider et al. 2014) and more realistic 3D models of vegetation elements potentially obtainable by terrestrial laser scanning. An application to forest management planning is described in the present study, but the modeling approach could also be suited for other applications requiring geometrically explicit parameterizations of forest landscapes. An example is light interaction and radiative transfer modeling (e.g., Schneider et al. 2014), in which incorrect assumptions on crown shapes and inappropriate voxel grid resolutions are reported to result in significant errors in retrieved crown parameters (Calders et al. 2013; Widlowski et al. 2014).

Visualization is a straightforward application for the triangulations and filtrations of ALS data collected over a forested area, which are earlier tested in various forest inventory applications (Vauhkonen et al. 2014, 2016; Vauhkonen 2015). As opposed to the typical "surface modeling" approaches using 2D to 2.5D raster images, the use of triangulations and filtrations provides means of constructing genuine 3D parameterizations of forested landscapes instead of just representing counts of height values within pixel or voxel cells. Besides triangulations, geometric modeling techniques that could be considered for solving the presented problem are an iterative surface wrapping technique based on delineated tree crowns (Kato et al. 2009), 3D clustering followed by convex polytope reconstruction (Gupta et al. 2010), stacking horizontal slices of the height values (Tang et al. 2013), or voxel-based techniques (Schneider et al. 2014; see also Koch et al. 2014). All these methods involve certain parameters to be set by the operator, and the obtained results depend on these. Further, the methods are so far tested with data densities varying from 4 to 5 m⁻² (Gupta et al. 2010) to 10–20 m⁻² (Kato et al. 2009; Tang et al. 2013; Schneider et al. 2014) as opposed to 0.8 m⁻² of this study. The data studied here would have resulted in an extremely coarse voxel grid resolution. On the other hand, requiring data with a higher density would mean distinct data acquisitions and therefore considerably higher inventory costs.

Applying filtrations, one can adjust the level of detail in the triangulated point cloud and thus account for canopy gaps and detailed properties existing in the data, which is controlled by filtration parameter α. The approaches to determine the filtration parameter have included using the most feasible population-specific fixed value like in Vauhkonen et al. (2012), who evaluated a range of α's, but rather than selecting one particular value, they used metrics quantifying the difference of the shape obtained with the range of α's to the convex hull of the point data, which corresponds to α-shapes with α → ∞. Vauhkonen et al. (2014, 2016) optimized the degree of filtration with respect to field-measured forest attributes and predicted this degree by means of linear regression. In the present study, the selection of α was based on analyzing the persistent homology of the filtrations (Edelsbrunner et al. 2002). This approach resulted in less accurate parameter estimates (e.g., R ² = 0.26 of the volumes in the present study vs. 0.49–0.83 reported in the previous studies) but eliminated the need for a field training data required for the optimization (Vauhkonen et al. 2014, 2016).

The persistent homology approach was tested to replace the calibration field data by analyzing the inherent topological properties of the point data. A simple approach based on the birth and death diagrams of the various simplices (Edelsbrunner et al. 2002) turned out to produce reasonably good information. The persistent homology of vegetation point clouds should be more comprehensively analyzed after this initial test. For example, one could derive the Euler characteristic and the Betti numbers from the filtrations (Robins 2002) and use them in a similar manner than the birth and death diagram was used. One could further attempt to quantify the obtained filtration by other geometric features than total volumes such as edge lengths or facet areas. The approach has a profound mathematical formalism on topological connectivity and implementations based on efficient data structures are available (Pion and Teillaud 2013; Da et al. 2013).

A definite difference and a strength of the triangulation-based approach over alternative 3D modeling or description techniques is the ability to simulate changes to the geometric models obtained. This is an inherent property of the technique adopted and may be simply implemented by adjusting the degree of filtering, but, to the best of our knowledge, this option has not been utilized elsewhere beyond the present study. Here, it was used to depict impacts of biomass harvesting to the scenic values of the area by simulating harvests with varying intensities. According to the high CR values, some incoherence existed in the pairwise comparisons, which can possibly be explained by a comparison of Figs. 3 and 4. According to Fig. 3, the reduction of the α value changed the top height of the canopy models based on harvesting intensities A, B, and C moderately, whereas the reduction of the top height was clearly more pronounced for harvests D and E. This corresponds well with the dispersion between A, B, and C as the most preferred harvesting intensity and the clearly lower preference toward D and E (Fig. 4). Although the canopy coverage changed more than height (Fig. 3), the moderate change in the top height may have dominated especially in the landscape scale considered. To generate more discriminative differences, either more intense harvests or fewer harvesting intensities should have been simulated.

The height and cover reduction of the simulated harvests (Fig. 3) can be compared to Nijland et al. (2015), who studied ALS data acquired from an experimental forest, where variable retention harvests had been replicated for different stands. Their observations on the behavior of maximum ALS echo height are fundamentally similar than our results illustrated in Fig. 3. Obviously, our technique cannot reproduce variations in the spatial pattern of the remaining trees caused by machine corridors and tree selection, for example, and the overall correspondence of the simulations with real-world harvests can only be validated under a rarely available experimental setup similar to Nijland et al. (2015). However, producing at least indicative information on the average reduction of tree height and cover corresponding to harvests with varying retention levels by just adjusting the degree of filtering would considerably facilitate similar simulations due to the simplicity of implementing this procedure.

Considering other possible explanations for the inconsistencies in the pairwise comparisons, it is possible that the respondent focused on other issues than scenic values such as a minimum timber recovery obtainable by the harvest or the concept of recreational or scenic values was not only affected by the harvesting intensity but issues such as the visibility from or to the walking path affected by logging trails, residues, stumps, etc. According to our tests, even a small inconsistency in just one of the comparisons could increase the CR above the threshold of 0.1. Similar problems are reported in ratio-scale pairwise comparisons based on other types of surveys (Sironen et al. 2013), and other measures have been presented for evaluating the inconsistencies (Peláez and Lamata 2003; Ramík and Korviny 2010) and uncertainties related to the process overall (see Alho and Kangas 1997), differing from those originally proposed by Saaty (1980).

According to the earlier studies on the preferences on forest use, the majority of citizens, regardless of forest ownership, do not approve of clearcutting (Valkeapää and Karppinen 2013). Also, according to pairwise comparisons of edited photographs of various forest management alternatives (Silvennoinen et al. 2002; Tönnes et al. 2004; Ribe 2009), the scenic values in clearcut forests are consistently lower than in forests grown in denser, uneven-aged structures. Yet, it should be noted that the studies mentioned in the previous sentence estimated preferences for alternatives of clear cuttings, such as seedling tree or retention tree harvests, and were thus examined at initially very low tree densities and using close-range visualizations. Overall, the scenic values are found to be lowest in both clearcut areas and in extremely dense, unthinned forests (Silvennoinen et al. 2001). Taken together with the earlier studies, the results obtained here become more logical: The heaviest harvesting intensities were deemed less attractive, while the preferences on the harvests leaving more standing trees varied. The results of the AHP thus support the realism of the landscapes generated.

Based on the discussion above, our approach is concluded to implement the main feature for a visualization system to support forestry decision making in the temporal dimension, i.e., the ability to represent the current and future texture of the trees in a geometric complexity that is possible to implement in a landscape extent (Falcão 2008). According to Falcão (2008), a missing key element is soil texturing, in which roads, tracks, human constructions, and other massive-scale characteristics are most important. Considering that these elements are usually obtained by overlaying satellite or aerial imagery over a digital elevation model (DEM), a potentially simple means to implement the description of the ground texture would be to export the canopy elements produced by our approach to an existing visual environment such as Google Earth. We acknowledge that also the visualization of the canopy elements could be considerably improved, for instance, using detailed lightning models that affect not only the vegetation but also the entire landscape. In a closely related study, Lämås et al. (2015) used photographs of tree and ground texture in a specific visualization software to generate scenes of future management rotations simulated for over 200-year periods. However, the trees in the landscapes were parameterized by only a few general attributes like vegetation height, density, and species. Our visualizations were contrariwise based on observed canopy geometry with less attention on the photorealism. Whether it is more important to focus on the realism in appearances or other properties likely depends on application and should be further analyzed particularly with respect to the information obtained for decision making.

As indicated in Sect. 1, we would like to emphasize the role of information already obtainable by the simple visualizations presented in this study. Once derived, the preferential information could be incorporated as an objective on choice of treatments for compartments in numerical optimization (Pukkala et al. 1995). Such information may become more valuable as situations where multi-attribute comparisons are required become more frequent (e.g., Pukkala et al. 2011). Even though ALS data are increasingly employed in operational inventories providing input for forest management planning (e.g., Næsset 2014), the aim of these inventories is typically limited to predicting conventional standwise forest mensurational attributes. Although the horizontal information on the distribution of forest patches is employed in spatial optimization (see, e.g., Pukkala et al. 2014) and integrating expert opinion with ALS data is noted to provide enhanced information (Pascual et al. 2013), no other decision support tools routinely used in forest management planning (Kangas et al. 2008) are common in analyses based on ALS data. The derivation of the preference information from the point data could thus be seen as an important contribution to the literature of using ALS data for forestry decision support.

Conclusion

The modeling approach proposed provided canopy elements that were fairly accurately co-located with the tree stems, but in a low numerical correspondence with plot-level forest attributes measured in the field. The visualization technique thus allowed close-range visualizations, but due to the coarse level of detail, better results were obtained at a landscape level. In turn, the approach can be operated based on ALS and field data, which already cover broad areas and are readily available for practical inventories.

The landscape-level visualizations produced were found to preserve a reasonable level of detail and realism. Except for static images depicting the present state of the canopy, the approach allowed simulating changes to the landscape, which were found to realistically resemble harvests with varying retention levels. Although the criteria to evaluate the visualization and simulation models were not conclusive, potential reasons were pointed out in the discussion.

Multicriteria decision analysis techniques such as the pairwise comparisons and the AHP allowed eliciting specific weights for each considered harvesting alternative, which are easy to incorporate into numerical optimization and forest management planning overall. Here, the heaviest intensities were deemed less attractive than lower ones, which support the previous research on preferences among management alternatives with respect to scenic amenity. According to the results of this study, the information obtainable directly from the ALS point data could be more integrally used for forest management planning.

References

• Ahlberg S, Söderman U, Elmqvist M, Persson Å (2004) On modelling and visualisation of high resolution virtual environments using lidar data. In: Proceedings of the 12th International Conference on Geoinformatics. University of Gävle, Sweden, pp 299–306

• Alho JM, Kangas J (1997) Analyzing uncertainties in experts' opinions of forest plan performance. For Sci 43:521–528

  Google Scholar

• Aono M, Kunii TL (1984) Botanical tree image generation. IEEE Comput Graph Appl 4:10–34

  Article  Google Scholar

• Baddeley A, Turner R (2005) Spatstat: an R package for analyzing spatial point patterns. J Stat Softw 12:1–42

  Article  Google Scholar

• Bergen SD, McGaughey RJ, Fridley JL (1998) Data-driven simulation, dimensional accuracy and realism in a landscape visualization tool. Landscape Urban Plan 40:283–293

  Article  Google Scholar

• Burkhart HE (1992) Scientific visualization for the study and use of forest stand simulators. Landscape Urban Plan 21:317–318

  Article  Google Scholar

• Calders K, Lewis P, Disney M, Verbesselt J, Herold M (2013) Investigating assumptions of crown archetypes for modelling LiDAR returns. Remote Sens Environ 134:39–49

  Article  Google Scholar

• Clark PJ, Evans FC (1954) Distance to nearest neighbour as a measure of spatial relationships in populations. Ecology 35:445–453

  Article  Google Scholar

• Da TKF, Loriot S, Yvinec M (2013) 3D alpha shapes. In: CGAL Editorial Board (ed) CGAL User and Reference Manual, 4.3 edition. http://doc.cgal.org/4.3/Manual/packages.html#PkgAlphaShapes3Summary. Accessed 2 Sept 2013

• Delfinado CJA, Edelsbrunner H (1995) An incremental algorithm for Betti numbers of simplicial complexes on the 3-sphere. Comput Aided Geom D 12:771–784

  Article  Google Scholar

• Donnelly K (1978) Simulations to determine the variance and edge-effect of total nearest neighbour distance. In: Hodder I (ed) Simulation studies in archaeology. Cambridge University Press, Cambridge/New York, pp 91–95

  Google Scholar

• Dreyfus P (2012) Joint simulation of stand dynamics and landscape evolution using a tree-level model for mixed uneven-aged forests. Ann For Sci 69:283–303

  Article  Google Scholar

• Duncanson LI, Cook BD, Hurtt GC, Dubayah RO (2014) An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens Environ 154:378–386

  Article  Google Scholar

• Edelsbrunner H, Mücke EP (1994) Three dimensional alpha-shapes. ACM Trans Graph 13:43–72

  Article  Google Scholar

• Edelsbrunner H, Letscher D, Zomorodian A (2002) Topological persistence and simplification. Discrete Comput Geom 28:511–533

  Article  Google Scholar

• Falcão AO (2008) Visualization in the design of forested landscapes. In: Gadow K, Pukkala T (eds) Designing green landscapes. Managing Forest ecosystems 15. Springer, Dordrecht, pp 245–263

  Chapter  Google Scholar

• Fujisaki I, Evans DL, Moorhead RJ, Irby DW, Mohammadi-Aragh MJ, Roberts SD, Gerard PD (2008) Stand assessment through lidar-based forest visualization using immersive virtual environment technology. For Sci 54:1–7

  Google Scholar

• Gaveau DLA, Hill RA (2003) Quantifying canopy height underestimation by laser pulse penetration in small-footprint airborne laser scanning data. Can J Remote Sens 29:650–657

  Article  Google Scholar

• Gupta S, Weinacker H, Koch B (2010) Comparative analysis of clustering-based approaches for 3-D single tree detection using airborne fullwave Lidar data. Remote Sens 2:968–989

  Article  Google Scholar

• Hill RA, Veitch N (2002) Landscape visualization: rendering a virtual reality simulation from airborne laser altimetry and multi-spectral scanning data. Int J Remote Sens 23:3307–3309

  Article  Google Scholar

• Honjo T, Lim EM (2001) Visualization of landscape by VRML system. Landscape Urban Plan 55:175–183

  Article  Google Scholar

• Kangas J, Store R (2003) Internet and teledemocracy in participatory planning of natural resources management. Landscape Urban Plan 62:89–101

  Article  Google Scholar

• Kangas J, Laasonen L, Pukkala T (1993) A method for estimating forest landowner's landscape preferences. Scand J For Res 8:408–417

  Article  Google Scholar

• Kangas A, Kangas J, Kurttila M (2008) Decision support for forest management. Managing Forest ecosystems 16. Springer, Dordrecht

  Google Scholar

• Karjalainen E, Tyrväinen L (2002) Visualization in forest landscape preference research: a Finnish perspective. Landscape Urban Plan 59:13–28

  Article  Google Scholar

• Kato A, Moskal LM, Schiess P, Swanson ME, Calhoun D, Stuetzle W (2009) Capturing tree crown formation through implicit surface reconstruction using airborne Lidar data. Remote Sens Environ 113:1148–1162

  Article  Google Scholar

• Koch B, Kattenborn T, Straub C, Vauhkonen J (2014) Segmentation of forest to tree objects. In: Maltamo M, Næsset E, Vauhkonen J (eds) Forestry applications of airborne laser scanning—concepts and case studies. Managing Forest ecosystems 27. Springer, Dordrecht, pp 89–112

  Chapter  Google Scholar

• Korhonen L, Korpela I, Heiskanen J, Maltamo M (2011) Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens Environ 115:1065–1080

  Article  Google Scholar

• Korpela I, Hovi A, Morsdorf F (2012) Understory trees in airborne LiDAR data—selective mapping due to transmission losses and echo-triggering mechanisms. Remote Sens Environ 119:92–104

  Article  Google Scholar

• Laasasenaho J (1982) Taper curve and volume functions for pine, spruce and birch. Comm Inst For Fenn 108:1–74

  Google Scholar

• Lämås T, Sandström E, Jonzén J, Olsson H, Gustafsson L (2015) Tree retention practices in boreal forests: what kind of future landscapes are we creating? Scand J For Res 30:526–537

  Article  Google Scholar

• Maltamo M, Packalén P, Yu X, Eerikäinen K, Hyyppä J, Pitkänen J (2005) Identifying and quantifying structural characteristics of heterogeneous boreal forests using laser scanner data. For Ecol Manag 216:41–50

  Article  Google Scholar

• Maltamo M, Næsset E, Vauhkonen J (eds) (2014) Forestry applications of airborne laser scanning—concepts and case studies. Managing Forest Ecosystems 27. Springer, Dordrecht

  Google Scholar

• McGaughey RJ, Carson WW (2003) Fusing LIDAR data, photographs, and other data using 2D and 3D visualization techniques. In: Proceedings of Terrain Data: Applications and Visualization, pp 28–30

• Mendoza G, Song B, Mladenoff D (2006) Visualization with spatial data. In: Shao G, Reynolds K (eds) Computer applications in sustainable Forest management. Managing Forest ecosystems 11. Springer, Dordrecht, pp 127–142

  Chapter  Google Scholar

• Morozov D (2012) Dionysus, a C++ library for computing persistent homology. http://mrzv.org/software/dionysus/. Accessed 6 Oct 2014

• Næsset E (2014) Area-based inventory in Norway—from innovation to an operational reality. In: Maltamo M, Næsset E, Vauhkonen J (eds) Forestry applications of airborne laser scanning—concepts and case studies. Managing Forest Ecosystems 27. Springer, Dordrecht, pp 215–240

  Chapter  Google Scholar

• Nijland W, Coops NC, Macdonald SE, Nielsen SE, Bater CW, Stadt JJ (2015) Comparing patterns in forest stand structure following variable harvests using airborne laser scanning data. For Ecol Manag 354:272–280

  Article  Google Scholar

• Nord-Larsen T, Schumacher J (2012) Estimation of forest resources from a country wide laser scanning survey and national forest inventory data. Remote Sens Environ 119:148–157

  Article  Google Scholar

• Packalén P, Vauhkonen J, Kallio E, Peuhkurinen J, Pitkänen J, Pippuri I, Strunk J, Maltamo M (2013) Predicting the spatial pattern of trees with airborne laser scanning. Int J Remote Sens 34:5154–5165

  Article  Google Scholar

• Pascual C, García-Montero LG, Arroyo LA, García-Abril A (2013) Increasing the use of expert opinion in forest characterisation approaches based on LiDAR data. Ann For Sci 70:87–99

  Article  Google Scholar

• Peláez JI, Lamata MT (2003) A new measure of consistency for positive reciprocal matrices. Comput Math Appl 46:1839–1845

  Article  Google Scholar

• Pion S, Teillaud M (2013) 3D triangulations. In: CGAL Editorial Board (ed) CGAL User and Reference Manual, 4.3 edition. http://doc.cgal.org/4.3/Manual/packages.html#PkgTriangulation3Summary. Accessed 2 Sept 2013

• Pukkala T, Kellomäki S (1988) Simulation as a tool in designing forest landscape. Landscape Urban Plan 16:253–260

  Article  Google Scholar

• Pukkala T, Nuutinen T, Kangas J (1995) Integrating scenic and recreational amenities into numerical forest planning. Landscape Urban Plan 32:185–195

  Article  Google Scholar

• Pukkala T, Lähde E, Laiho O, Salo K, Hotanen JP (2011) A multifunctional comparison of even-aged and uneven-aged forest management in a boreal region. Can J For Res 41:851–862

  Article  Google Scholar

• Pukkala T, Packalén P, Heinonen T (2014) Dynamic treatment units in forest management planning. In: Borges JG, Diaz-Balteiro L, McDill ME, Rodriguez LCE (eds) The Management of Industrial Forest Plantations. Managing Forest Ecosystems 33. Springer, Dordrecht, pp 373–392

  Google Scholar

• Ramík J, Korviny P (2010) Inconsistency of pairwise comparison matrix with fuzzy elements based on geometric mean. Fuzzy Sets Syst 161:1604–1613

  Article  Google Scholar

• Ribe RG (2009) In-stand scenic beauty of variable retention harvest and mature forests in the U.S Pacific northwest: the effects of basal area, density retention pattern and down wood. J Env Manage 91:245–260

  Article  Google Scholar

• Robins V (2002) Computational topology for point data: Betti numbers of α-shapes. In: Morphology of Condensed Matter. Lect Notes Phys 600:261–274

• Saaty TL (1977) A scaling method for priorities in hierarchical structures. J Math Psychol 15:234–281

  Article  Google Scholar

• Saaty TL (1980) The analytic hierarchy process. Planning, priority setting, resource allocation. McGraw-Hill, New York

  Google Scholar

• Schneider FD, Leiterer R, Morsdorf F, Gastellu-Etchegorry JP, Lauret N, Pfeifer N, Schaepman ME (2014) Simulating imaging spectrometer data: 3D forest modeling based on LiDAR and in situ data. Remote Sens Environ 152:235–250

  Article  Google Scholar

• Sieber R (2006) Public participation and geographic information systems: a literature review and framework. Ann Amer Ass Geogr 96:491–507

  Article  Google Scholar

• Silvennoinen H, Alho J, Kolehmainen O, Pukkala T (2001) Prediction models of land-scape preferences at the forest stand level. Landscape Urban Plan 56:11–20

  Article  Google Scholar

• Silvennoinen H, Pukkala T, Tahvanainen L (2002) Effect of cuttings on the scenic beauty of a tree stand. Scand J For Res 17:263–273

  Article  Google Scholar

• Simons L, He S, Tittman P, Amenta N (2014) Point-based rendering of forest LiDAR. In: Workshop on Visualisation in Environmental Sciences (EnvirVis), The Eurographics Association, pp 19–23

• Sironen S, Leskinen P, Kangas A, Hujala T (2013) Variation of preference inconsistency when applying ratio and internal scale pairwise comparisons. J Multi-Criteria Decis Anal 21:183–195

  Article  Google Scholar

• Store R, Kangas J (2001) Integrating spatial multi-criteria evaluation and expert knowledge for GIS-based habitat suitability modelling. Landscape Urban Plan 55:79–93

  Article  Google Scholar

• Sun G, Ranson KJ (2000) Modelling Lidar returns from forest canopies. IEEE Trans Geosci Remote Sens 38:2617–2626

  Article  Google Scholar

• Tahvanainen L, Tyrväinen L, Ihalainen M, Vuorela N, Kolehmainen O (2001) Forest management and public perceptions—visual versus verbal information. Landscape Urban Plan 53:53–70

  Article  Google Scholar

• Tang S, Dong P, Buckles BP (2013) Three-dimensional surface reconstruction of tree canopy from lidar point clouds using a region-based level set method. Int J Remote Sens 34:1373–1385

  CAS  Article  Google Scholar

• Tönnes S, Karjalainen E, Löfström I, Neuvonen M (2004) Scenic impacts of retention trees in clear-cutting areas. Scand J For Res 19:348–357

  Article  Google Scholar

• Uusitalo J, Orland B (2001) Virtual forest management: possibilities and challenges. Int J For Eng 12:57–66

  Google Scholar

• Valkeapää A, Karppinen H (2013) Citizens' view of legitimacy in the context of Finnish forest policy. For Pol Econ 28:52–59

  Article  Google Scholar

• Vauhkonen J (2015) Reconstruction, quantification, and visualization of forest canopy based on 3D triangulations of airborne laser scanning point data. In: Stilla U, Heipke C (eds) PIA15 + HRIGI15 – Joint ISPRS Conference. ISPRS Ann Photogramm Remote Sens Spatial Inf Sci II-3/W4:255–261

• Vauhkonen J, Seppänen A, Packalén P, Tokola T (2012) Improving species-specific plot volume estimates based on airborne laser scanning and image data using alpha shape metrics and balanced field data. Remote Sens Environ 124:534–541

  Article  Google Scholar

• Vauhkonen J, Næsset E, Gobakken T (2014) Deriving airborne laser scanning based computational canopy volume for forest biomass and allometry studies. ISPRS J Photogramm Remote Sens 96:57–66

  Article  Google Scholar

• Vauhkonen J, Holopainen M, Kankare V, Vastaranta M, Viitala R (2016) Geometrically explicit description of forest canopy based on 3D triangulations of airborne laser scanning data. Remote Sens Environ 173:248–257

  Article  Google Scholar

• Villikka M, Packalén P, Maltamo M (2012) The suitability of leaf-off airborne laser scanning data in an area-based forest inventory of coniferous and deciduous trees. Silva Fenn 46:99–110

  Article  Google Scholar

• Wang X, Song B, Chen J, Crow T, LaCroix J (2006) Challenges in visualizing forests and landscapes. J For 104:316–319

  Google Scholar

• Warren-Kretzschmar B, von Haaren C (2014) Communicating spatial planning decisions at the landscape and farm level with landscape visualization. iForest-Biogeosci For 7:434–442

  Article  Google Scholar

• Widlowski JL, Côté JF, Béland M (2014) Abstract tree crowns in 3D radiative transfer models: impact on simulated open-canopy reflectances. Remote Sens Environ 142:155–175

  Article  Google Scholar

Download references

Author information

Author notes

1. Jari Vauhkonen

   Present address: Natural Resources Institute Finland (Luke), Economics and Society, Yliopistokatu 6, P.O. Box 68, FI-80101, Joensuu, Finland

Authors and Affiliations

1. School of Forest Sciences, University of Eastern Finland, Yliopistokatu 7, P.O. Box 111, FI-80101, Joensuu, Finland

   Jari Vauhkonen & Roope Ruotsalainen

2. Department of Forest Sciences, University of Helsinki, Latokartanonkaari 7, P.O. Box 27, FI-00014, Helsinki, Finland

   Jari Vauhkonen & Roope Ruotsalainen

Corresponding author

Correspondence to Jari Vauhkonen.

Ethics declarations

Funding

This study was supported by the Research Funds of the University of Helsinki.

Additional information

Contribution of the co-authors Jari Vauhkonen designed the study, implemented all stages related to reconstructing the forest scenes, and drafted the manuscript.

Roope Ruotsalainen carried out the survey and analyzed its results with pairwise comparisons and the analytic hierarchy process. He also read and approved the final manuscript.

Handling Editor: Jean-Michel Leban

Electronic supplementary material

Online Resource 1

Simulated landscapes with harvesting intensities A-E. (DOCX 2924 kb).

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and Permissions

About this article

Cite this article

Vauhkonen, J., Ruotsalainen, R. Reconstructing forest canopy from the 3D triangulations of airborne laser scanning point data for the visualization and planning of forested landscapes. Annals of Forest Science 74, 9 (2017). https://doi.org/10.1007/s13595-016-0598-6

Download citation

• Received: 15 March 2016

• Accepted: 04 November 2016

• Published: 06 February 2017

• DOI : https://doi.org/10.1007/s13595-016-0598-6

Keywords

• Spatial multicriteria decision analysis
• Public participation geographic information system (PPGIS)
• Remote sensing
• Light detection and ranging (LiDAR)
• Persistent homology
• Alpha shape

ringgoldnobster.blogspot.com

Source: https://annforsci.biomedcentral.com/articles/10.1007/s13595-016-0598-6

Share this post